Principe de construction géométrique
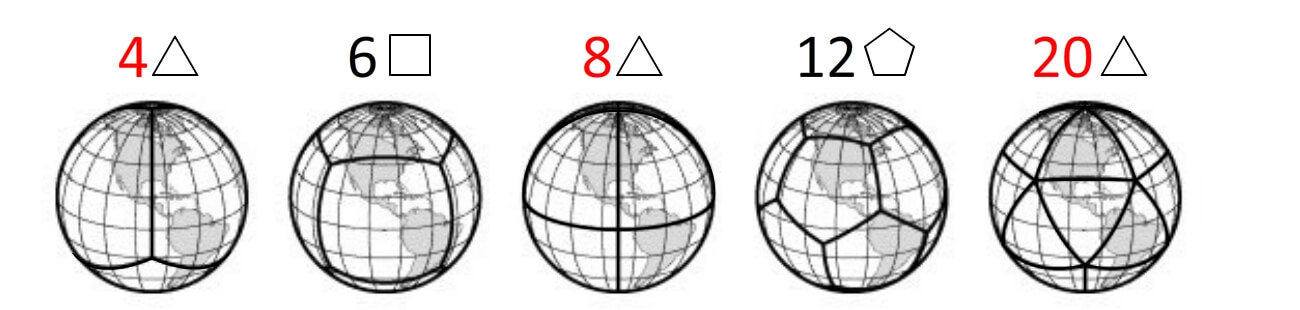
On part de la forme que nous souhaitons reproduire : une sphère, que l'on divise en surfaces égales. 5 découpages sont possibles, lequel choisir ?
Structurellement, géométriquement, le triangle est la forme la plus indéformable qui soit, la plus robuste. Chaque triangle d'un dôme possède sa propre rigidité, provoquant la distribution des forces et des tensions sur l'ensemble de la structure, qui est de ce fait autoporteuse. Une force exercée sur un sommet ou un triangle sera donc homogènement transmise et diluée sur tous les autres triangles.
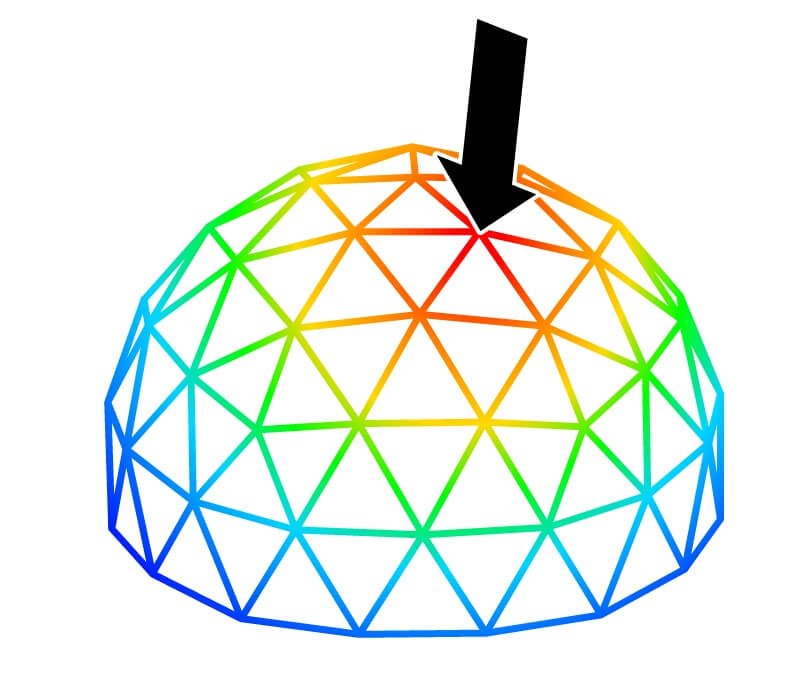
Choisissons alors le découpage en 20 triangles, et transformons les lignes courbes en lignes droites ; on obtient un icosaèdre à 20 faces triangulaires (un des 5 solides de Platon). Ce volume est une approximation de la sphère. Pour améliorer cette approximation, il ne reste plus qu'à densifier le nombre de triangles (= augmenter la fréquence) pour créer des géodes, ou sphères géodésiques. Plus la fréquence augmente, plus on se rapproche de la forme d'une sphère. Et enfin, les dômes géodésiques sont une partie de ces sphères géodésiques (généralement la moitié).
Nous avons ainsi réussi à créer une structure de forme quasi sphérique en utilisant des arêtes droites constituées en la forme la plus indéformable : le triangle !
Le dôme géodésique est la rencontre entre la beauté du rond et la solidité du triangle.
Le prix à payer pour tous ces avantages est une plus grande complexité dans la réalisation de la couverture du dôme. Que ça soit avec une toile ou des panneaux, il y a une centaine de triangles à recouvrir, chacun dans un plan différent des voisins, (là où il n'y a qu'une grande surface plane pour une construction rectangulaire). D'autre part il est également plus difficile d'intégrer des portes (rectangulaires) que dans une construction classique.
